Is my gym locker more likely to be prime?

So, before I was developer educator I was a developer, before that I was an educator - specifically a Maths teacher. I worked with 11-18 year olds and tried, sometimes successfully, to make Maths interesting and engaging. I worked hard to help previously Math-phobic and Math-philic(?) students develop a growth mindset.

While teaching, I’d be constantly looking at my life and trying to find examples and uses, patterns and problems I could invite into the classroom.

I do this now as a developer educator but every once in a while my brain starts asking Maths related questions.

That happened while standing in the gym lockers earlier this week.

I was looking at the lockers and wondering if my locker was more likely to be prime than any other locker. I always go for lockers on the middle row. It’s the right height for me to reach, don’t have to bend down or stretch up.

So, the first thing I had to do was to work out a way to represent the middle row.

Well, that’s a linear sequence. Goes up in 3s so it is some multiple of 3. So, the formula has 3n in it.

3n: 0, 3, 6, 9, …

To make that pattern match my lockers though, I need to add on 2. So, the formula is 3n + 2.

Now, which of the lockers is prime?

So, for 15 lockers, the middle row is more likely to be prime. But what about for 100 lockers?

So, the bottom row is the multiples of 3. That means only the first one is prime. Even if the lockers go off to infinity, then the bottom row will stay white.

The of the other two rows then, 3n + 1 and 3n + 2, which is more likely to be prime?

What would be helpful here is to have a table or a graph to see this.

Number of columns	3n + 1	3n + 2
3	1	2
30	?	?

I don’t know about you but I don’t want to count those - that’s what computers are for!

Fair warning - my algorithm isn’t super efficient so I’m going to cap it at 10,000. Otherwise, it might crash this page.

Number of columns:

Number of primes in the top row: 1 (probability 10%)

Number of primes in the middle row: 2 (probability 20%)

And here’s a graph of the same data to even bigger numbers. This graph has two lines showing the probability for the top and the middle row.

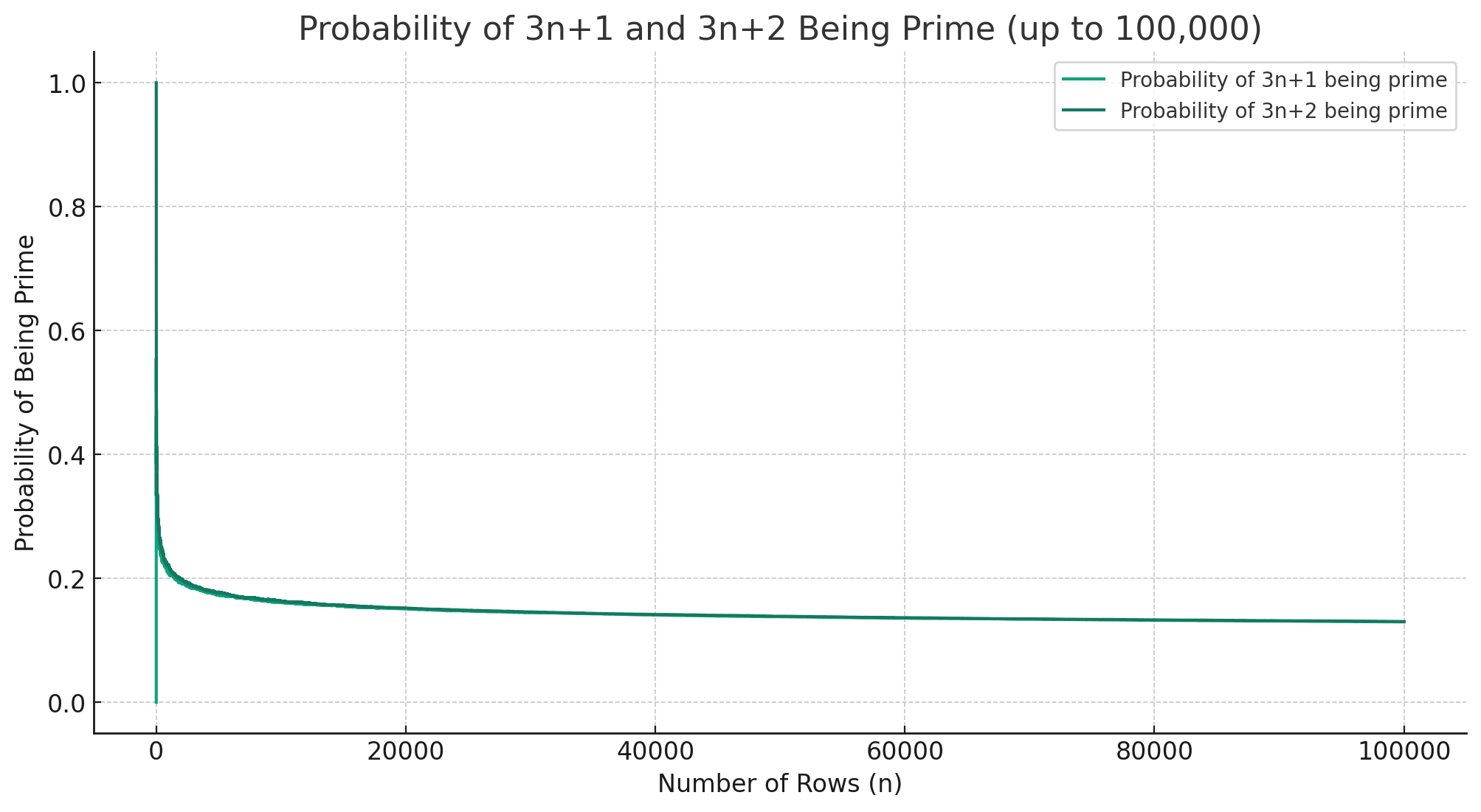
So, as the numbers get bigger it is more likely for the middle row to be prime but only just.

I’ve taken this thought experiment as far as I want to right now. I could use formal proof and have fun with that.

For now though, it’s been fun to remember that this part of my brain exists and that I can still use it. I could definitely turn this into a few hours of lessons with my old classes. I don’t teach Maths any more, so you’ll all have to do!